Neural networks are computing systems inspired by the human brain. They consist of interconnected units called neurons, which process information similarly to the way our own brains do. At their core, neural networks learn to recognize patterns and make decisions by adjusting connections between these neurons. This learning process is driven by math, particularly by equations that describe how signals flow and how errors are minimized.

Structure of a Neural Network

A neural network is typically organized into layers:

1. Input Layer: This is where the network receives data. Each neuron in the input layer represents a feature of the problem you want to solve.
2. Hidden Layers: These layers perform intermediate computations. A simple network might have one hidden layer, while more advanced models can have several.
3. Output Layer: This layer produces the result, whether it is a classification (like “cat” or “dog”) or a predicted number.

Each neuron computes a weighted sum of its inputs and adds a bias term. Mathematically, for a single neuron, this is represented as:

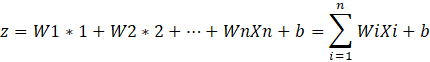
Here,

• Xi are the inputs,
• Wi are the weights,
• b is the bias,
• z is what we call the “net input” to the neuron.

After computing z, the neuron applies an activation function (f) to introduce non-linearity:

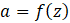
The output aa is then passed on to the next layer.

Activation Functions

Activation functions help the network learn complex patterns. Two common examples are:

1. Sigmoid Function: The sigmoid function squeezes input values into a range between 0 and 1:

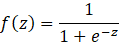
It is particularly useful for binary classification tasks.

2. ReLU (Rectified Linear Unit): The ReLU function outputs 0 if the input is less than 0, and it outputs the input directly if the input is greater than 0:

These functions allow neural networks to capture non-linear relationships in data.

The Feedforward Process

In a neural network, information flows forward from the input layer to the output layer. For a layer with multiple neurons, we can represent the computation using matrix notation. Suppose we have an input vector x, a weight matrix W (where each row corresponds to a neuron), and a bias vector b. The output of the layer is computed as:

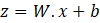
Then, the activation is applied elementwise to z:

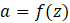
This process is repeated for every layer, moving from the input to the output.

Training the Network: Backpropagation and Gradient Descent

Once the network makes a prediction, we need a way to evaluate its performance. This is done with a loss function L, which measures the difference between the predicted output and the target output. A common choice is the Mean Squared Error (MSE) for regression tasks:

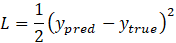
The goal of training is to minimize this loss. Backpropagation is the algorithm used to propagate the error back through the network and compute the gradient (a measure of how much each weight contributes to the error). Using gradient descent, we update each weight ww as follows:

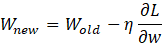
Here, n (eta) is the learning rate, controlling how fast the network learns. Similar updates are applied to the biases. The process of computing the partial derivative dL/dw leverages the chain rule from calculus, linking the change in loss back to changes in each weight.

This iterative adjustment continues until the network’s error is minimized to a satisfactory level.

To summarize, neural networks work by:

• Taking inputs and passing them through layers of neurons.
• Each neuron computes a weighted sum of its inputs, adds a bias, and applies an activation function.
• The network produces an output, which is compared to the desired target using a loss function.
• Using the backpropagation algorithm and gradient descent, the network adjusts its weights and biases to reduce the error.

Over many iterations (or epochs), the network “learns” the optimal weights that enable it to make accurate predictions.

Neural networks are powerful because they can model complex, non-linear relationships in data with simple yet flexible mathematical building blocks. As you explore further, you’ll find that there are many variations—such as convolutional neural networks (for image processing) or recurrent neural networks (for sequential data)—each built on the same fundamental principles.