Retinex is an image enhancement technique inspired by human vision. It separates an image into illumination and reflectance components to correct uneven lighting. It is based on the Retinex theory of color vision, which posits that the perceived color of an object is determined by its reflectance properties, rather than solely by the illumination it receives. 

Theory of Retinex:

Core Principle:

The fundamental idea behind Retinex is to decompose an observed image (I) into two components:

• Reflectance (R): This represents the intrinsic properties of the object’s surface, determining its color and texture.
• Illumination (L): This represents the varying light conditions across the scene.

The relationship is typically expressed as:  I = R * L.

To extract the reflectance component (R), the algorithm aims to estimate and remove the illumination component (L). This is often achieved by taking the logarithm of the equation: log(I) = log(R) + log(L).

Then, the reflectance can be estimated by subtracting the estimated illumination from the observed image in the logarithmic domain: log(R) = log(I) – log(L).

Reflectance vs. Illumination

• Reflectance: the inherent colors and details of objects.
• Illumination: the lighting effect across the scene.

Retinex estimates illumination and removes it, revealing true reflectance.

Single Scale Retinex (SSR)

• Uses one Gaussian filter of scale σ to estimate illumination.
• Output = log(input) – log (Gaussian (input, σ)).
• Fast but may produce halos around edges.

Multi Scale Retinex (MSR)

• Combines several SSR outputs at different σ values.
• Balances fine detail and global contrast.
• Formula:

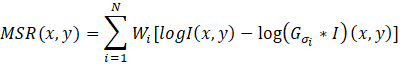
Color Restoration (MSRCR)

• Adds a gain–offset or ratio term to correct color distortions.
• Common form:

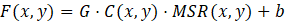
where C(x, y) is a color restoration factor.

Algorithm Steps

1. Convert image to floating point and add a small constant to avoid log (0).
2. For each scale σ:
   • Convolve image with Gaussian of σ.
   • Compute SSR: log(I) – log (blurred I).
3. Weight and sum SSR outputs for MSR.
4. (Optional) Apply color restoration and linear scaling.
5. Clip results to valid range and convert back to 8-bit.

C++ Implementation with OpenCV:

#include <opencv2/opencv.hpp>

#include <vector>

using namespace cv;

// Single Scale Retinex

Mat singleScaleRetinex(const Mat& src, double sigma) {

    Mat logI, blurI, dst;

    src.convertTo(logI, CV_32F, 1.0/255.0);

    log(logI + 1e-6, logI);

    GaussianBlur(logI, blurI, Size(), sigma, sigma);

    dst = logI – blurI;

    normalize(dst, dst, 0, 255, NORM_MINMAX);

    dst.convertTo(dst, CV_8UC1);

    return dst;

}

// Multi Scale Retinex

Mat multiScaleRetinex(const Mat& src, const std::vector<double>& sigmas,

                      const std::vector<double>& weights) {

    Mat srcGray, retinex;

    cvtColor(src, srcGray, COLOR_BGR2GRAY);

    retinex = Mat::zeros(srcGray.size(), CV_32F);

    for (size_t i = 0; i < sigmas.size(); ++i) {

        Mat ssr = singleScaleRetinex(srcGray, sigmas[i]);

        retinex += weights[i] * (ssr / 255.0f);

    }

    normalize(retinex, retinex, 0, 255, NORM_MINMAX);

    Mat output;

    retinex.convertTo(output, CV_8UC1);

    return output;

}

int main() {

    Mat img = imread(“input.jpg”);

    std::vector<double> sigmas = {15, 80, 250};

    std::vector<double> weights = {0.333, 0.333, 0.334};

    Mat result = multiScaleRetinex(img, sigmas, weights);

    imwrite(“msr_output.jpg”, result);

    return 0;

}

Python Implementation with OpenCV and NumPy:

import cv2

import numpy as np

def single_scale_retinex(img, sigma):

    img = img.astype(‘float32’) / 255.0

    log_img = np.log(img + 1e-6)

    blur = cv2.GaussianBlur(log_img, (0,0), sigma)

    retinex = log_img – blur

    return np.uint8(255 * (retinex – retinex.min())/(retinex.max() – retinex.min()))

def multi_scale_retinex(img, sigmas, weights):

    img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

    retinex = np.zeros_like(img_gray, dtype=’float32′)

    for sigma, weight in zip(sigmas, weights):

        ssr = single_scale_retinex(img_gray, sigma).astype(‘float32’) / 255.0

        retinex += weight * ssr

    retinex = cv2.normalize(retinex, None, 0, 255, cv2.NORM_MINMAX)

    return np.uint8(retinex)

if __name__ == “__main__”:

    img = cv2.imread(‘input.jpg’)

    sigmas = [15, 80, 250]

    weights = [1/3, 1/3, 1/3]

    msr = multi_scale_retinex(img, sigmas, weights)

    cv2.imwrite(‘msr_python.jpg’, msr)

Retinex algorithms are widely used for:

• Low-light image enhancement: Improving visibility and detail in images captured under poor lighting.
• Dynamic range compression: Making details visible in both bright and dark areas of an image.
• Color constancy: Achieving consistent color perception regardless of illumination changes.
• Medical imaging: Enhancing poorly visible structures in X-rays or scans.
• Astronomical imaging: Making faint details in celestial images more apparent.